不会制作教学数据分析模型，九数云来帮你 | 帆软九数云

九数云BI小编 | 发表于：2023-03-15 9:47:43

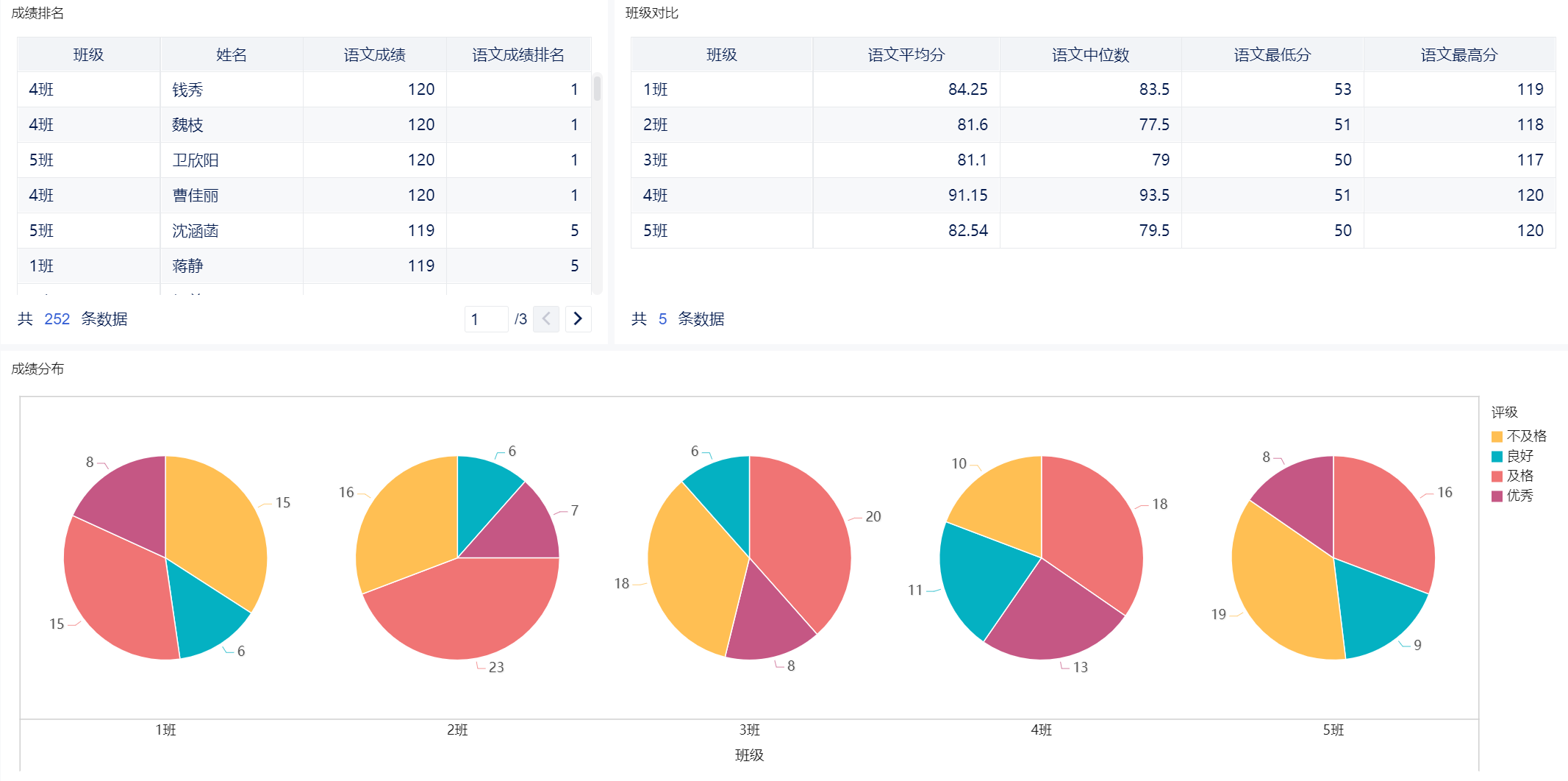
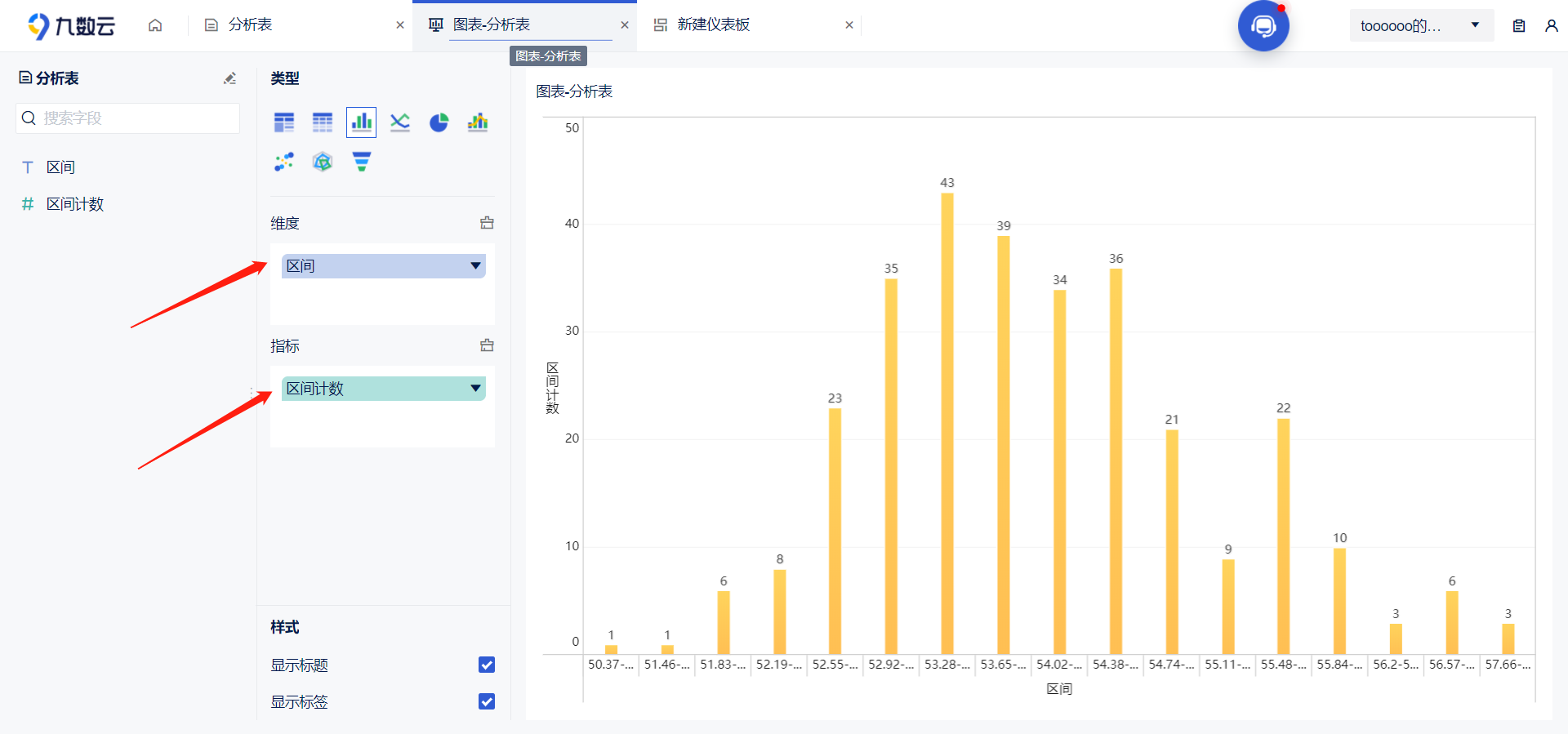
本节以学生的考试成绩为例，利用教学数据分析模型进行对考核对象的综合评价。

一、SPSS操作

教学数据分析模型的第一步，依次单击菜单“分析—降维—因子”执行因子分析过程，选取变量。

点击“描述”按钮，依次选系数、显著性水平、KMO 和巴特利特球形度检验，点击继续，返回主菜单。

单击“提取”按钮，勾选“碎石图”，其他选项默认，选择主成份法进行因子提取。单击“继续”按钮返回主面板。

单击旋转按钮，单击选中最大方差法单选框，表示采用方差最大旋转法进行因子旋转。单击继续按钮返回主面板。

单击得分按钮，勾选底部的显示因子得分系数矩阵复选框。单击继续按钮返回主面板。

设置完毕后，点击确定，生成结果。

二、结果分析

KMO检验和Bartlett球形检验。公因子提取的方差。给出了公因子对初始变量方差的提取情况，也就是常说的变量共同度。其中的“提取”栏就是变量共同度的取值，代表了所有公因子能够解释的每个变量方差的比例。

方差解释表。方差解释表给出了每个因子所解释的总方差比例，以及所解释方差的累计和。

最后一栏“旋转平方和载入”表示经过因子旋转后得到的新公因子的方差贡献值、方差贡献率和累计方差贡献率，可以看到和未经旋转相比，每个因子的方差贡献值有变化，但累计方差贡献率不变。

方差解释表，是关于初始特征值（也就是方差贡献）的碎石图。

旋转前后的因子载荷矩阵，给出了旋转前后的因子载荷矩阵，其中“成分矩阵”表是初始的未经旋转的载荷矩阵，“旋转成分矩阵”是经过旋转后的载荷矩阵。

因子得分的系数矩阵。输出的是因子得分系数矩阵。对于每个因子，把系数和对应的课程名称相乘后再求和，可以得到最终的因子得分公式，利用它就能够对所有案例进行教学数据分析模型中的因子评分了。

三、综合评分

如果要关心的是学生的综合能力，可对公因子的得分进行加权求和，权数就取其方差贡献值或方差贡献率。

通过前面的分析，利用教学数据分析模型已经得到了能够进行综合评分的公式，由此可以对学生成绩进行更为科学的判断和排序。

热门产品推荐

九数云BI是一个人人都可轻松上手的零代码工具，您可以使用它完成各类超大数据量、超复杂数据指标的计算，也可以在5分钟内创建富有洞察力的数据看板。企业无需IT、无需大量资源投入，就能像搭积木一样搭建企业级数据看板，全盘核心指标综合呈现，用数据驱动商业决策。

热门产品推荐